Tech Talk Notes

Tech Talk 3

Bubble Sort

Swaps adajcent elements into the correct order
Whole pass is then performed to ensure that the array is fully sorted, and the algorithm knows to stop
Time Complexity/ Big O Notation: Bubble sort can vary in its Big O Notation, with a worst case scenario of O(n^2) and a best case scenario of O(n)
Code which we built off of in the implementation process

package src.week3.SortTypes;
import java.util.*;

public class BubbleSort {
  public static void SortSortSort(List<Integer> list) {
    Integer temp;
    boolean sorted = false;

    while (!sorted) {
        sorted = true;
        for (int i = 0; i < list.size()-1; i++) {
            if (list.get(i).compareTo(list.get(i + 1)) > 0) {
                temp = list.get(i);
                list.set(i, list.get(i + 1));
                list.set(i + 1, temp);
                sorted = false;
            }
        }
    }
}
}

Implementation

Created individual file to contain the sorting algorithm developed
Utilized each sort as a method, which we use to sort the 5,000 element array when we use analyze()
Time is recorded each time we sort and added to an arraylist
- Using this list we can find total time, as well as the largest and smallest values and remove them if nessecary
Data is then displayed

Output

Selection Sort

Finds the minimun value element repeadly in an ascending pattern
Essentially has 2 arrays, in which the minimun value is then added to a sorted array, while algorithm finds the next minimun value in the unsorted array
Time Complexity Formula/ Big O Notation: O(n^2) is the notation because selection sort utilizes 2 arrays

Flowchart

Example algorithm of a selection sort which we built off of and implemented:

package src.week3.SortTypes;
import java.util.*;


public class SelectionSort {  
    public static void SortSortSort(ArrayList<Integer> arr){  
        for (int i = 0; i < arr.size() - 1; i++)  
        {  
            int index = i;  
            for (int j = i + 1; j < arr.size(); j++){  
                if (arr.get(j) < arr.get(index)){  
                    index = j; //searching for lowest index  
                }  
            }  
            int smallerNumber = arr.get(index);   
            arr.set(index, arr.get(i)); 
            arr.set(i, smallerNumber);  
        }  
    }  
}

Implementation

Implementation is similar to other sorts
Created individual file to contain the sorting algorithm developed
Utilized each sort as a method, which we use to sort the 5,000 element array when we use analyze()
Time is recorded each time we sort and added to an arraylist
- Using this list we can find total time, as well as the largest and smallest values and remove them if nessecary
Data is then displayed

Output

Merge Sort

Merge Sort is a divide and conquer type of algorithm
Input array is divided into 2 halves, calls each half, and then merges the halves back together
- Merge is the key process and is executed after the halves are sorted
Time Complexity/Big O Notation: O(n * Log (n)) Because this is a logarithmic function, it means that the time taken based on the amount of elements isn’t as affected, and is a rather efficent program. Even in a worst case scenario, the notation still reamins the same

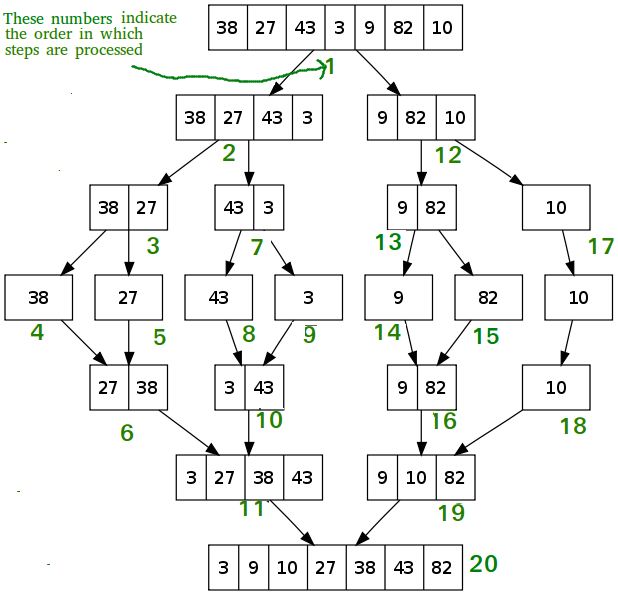
Flowchart

Sample algorithm which we built off to try and implement

package src.week3.SortTypes;
import java.util.ArrayList;
import java.util.Scanner;

public class MergeSort {
 
    private ArrayList<String> strList;
 
    public static void SortSortSort(ArrayList<Integer> whole) {
        ArrayList<Integer> left = new ArrayList<Integer>();
        ArrayList<Integer> right = new ArrayList<Integer>();
        int center;

            center = whole.size()/2;
            // copy the left half of whole into the left.
            for (int i=0; i<center; i++) {
                    left.add(whole.get(i));
            }
 
            //copy the right half of whole into the new arraylist.
            for (int i=center; i<whole.size(); i++) {
                    right.add(whole.get(i));
            }
 
            // Sort the left and right halves of the arraylist.
            left  = mergeSort(left);
            right = mergeSort(right);
 
            // Merge the results back together.
            merge(left, right, whole);
      

}



      public static ArrayList<Integer>mergeSort(ArrayList<Integer> whole) {
        ArrayList<Integer> left = new ArrayList<Integer>();
        ArrayList<Integer> right = new ArrayList<Integer>();
        int center;

        if (whole.size() == 1) {    
        return whole;
    } else {
          center = whole.size()/2;
            // copy the left half of whole into the left.
            for (int i=0; i<center; i++) {
                    left.add(whole.get(i));
            }
 
            //copy the right half of whole into the new arraylist.
            for (int i=center; i<whole.size(); i++) {
                    right.add(whole.get(i));
            }
 
            // Sort the left and right halves of the arraylist.
            left  = mergeSort(left);
            right = mergeSort(right);
 
            // Merge the results back together.
            merge(left, right, whole);
      
            return whole;
    }
            
}
 
    public static void merge(ArrayList<Integer> left, ArrayList<Integer> right, ArrayList<Integer> whole) {
        int leftIndex = 0;
        int rightIndex = 0;
        int wholeIndex = 0;
 
        // As long as neither the left nor the right ArrayList has
        // been used up, keep taking the smaller of left.get(leftIndex)
        // or right.get(rightIndex) and adding it at both.get(bothIndex).
        while (leftIndex < left.size() && rightIndex < right.size()) {
            if ( (left.get(leftIndex).compareTo(right.get(rightIndex))) < 0) {
                whole.set(wholeIndex, left.get(leftIndex));
                leftIndex++;
            } else {
                whole.set(wholeIndex, right.get(rightIndex));
                rightIndex++;
            }
            wholeIndex++;

Implementation

Implementation is similar to other sorts
Created individual file to contain the sorting algorithm developed
Utilized each sort as a method, which we use to sort the 5,000 element array when we use analyze()
Time is recorded each time we sort and added to an arraylist
- Using this list we can find total time, as well as the largest and smallest values and remove them if nessecary
Data is then displayed

Output

Insertion Sort

Uses 2 arrays, sorted and unsorted, and sorts the elements within the unsorted array and addes them to the sorted array
Time Complexity/Big O Notation: O(n). This means that the time taken to sort is directly proportional to the amount of elemenets sorted. However, this is only the best case scenario. On average, and in the worst case, the Big O Notation is O(n^2) which notates a longer time taken
Algorithm Breakdown:
- Iterate from arr[1] to arr[n] over the array.
- Compare the current element (key) to its predecessor.
- If the key element is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.

Flowchart

Algorithm we worked on implementing into the challenge

package src.week3.SortTypes;
import java.util.*;

public class InsertionSort {
  public static void SortSortSort(List<Integer> list) {
      for (int j = 1; j < list.size(); j++) {
          Integer current = list.get(j);
          int i = j-1;
          while ((i > -1) && (list.get(i) > current)) {
              list.set(i+1, list.get(i));
              i--;
          }
          list.set(i+1, current);
      }
  }
}

Implementation

Implementation is similar to other sorts
Created individual file to contain the sorting algorithm developed
Utilized each sort as a method, which we use to sort the 5,000 element array when we use analyze()
Time is recorded each time we sort and added to an arraylist
- Using this list we can find total time, as well as the largest and smallest values and remove them if nessecary
Data is then displayed

Output

(TPT) Study Group Challenge 2

Assignment:

Build a calculator to process expressions and ultimately change RPN to a calculation.
1. Build in Power of operator ^: 2 ^ 1 = 2, 2 ^ 2 = 4, 2 ^ 3 = 8
2. Extra credit. Build variable assignment and evaluation into your expressions (a = 2; a + 1).
3. Extra credit. Investigate Wikipedia article and pseudo code and try adding a SQRT(). Try building Pythagoras expression.

Tri 3: Tech Talk 2: Calculator

Math Symbols:

PEMDAS, each operator has its own precedence (priority)
- Add exponent ^ operator with priority 3

// Helper definition for supported operators
    private final Map<String, Integer> OPERATORS = new HashMap<>();
    {
        // Map<"token", precedence> 
        OPERATORS.put("*", 3);
        OPERATORS.put("/", 3);
        OPERATORS.put("%", 3);
        OPERATORS.put("+", 4);
        OPERATORS.put("-", 4);
    }

Math Original Expression (String):

2 + 2
4 * 6 + 3
5 + 1 * 8
(7 + 5) * 9

Tokenization (Array):

[2, +, 2]
[4, *, 6, +, 3]
[5, +, 1, *, 8]
[(, 7, +, 5, ), *, 9]

Reverse Polish Notation (Array, works well with Stack):

[2, 2, +]
[4, 6, *, 3, +]
[5, 1, 8, *, +]
[7, 5, +, 9, *]

Youtube Video

Sorting the values within the Reverse Polish Notation arrayList
- Is it an operator (+ - * / %)?
  - Is the existing operator of greater precedence?
    - Push to Stack
  - Else
    - Pop out operator underneath
    - Push to Stack
    - Push the popped operator back to Stack
- Is it a seperator (“ “)?
  - Skip it
- Is it a number (1 2 3 4 5)?
  - Put it in a Queue

Result (Double):

4.0
27.0
13.0
108.0

Tech Talk 1

Linked Lists

Most “Data Structures” conversations usually begin with Arrays
- Is built into most Computer Programming Languages
College Board has Units 6-8 which discuss Arrays, ArrayLists, and 2-Dimensional Arrays
Most Data Structures conversations continue with the discussions of Linked Lists which are the foundation for Stacks and Queues

Tech Talk 0

Data Structures

A data structure is a method of organizing data
Think of a variable holding a single integer value(ex: int n=4;) or sequences of numbers(ex: int[] numbers=new int[]{ 1,2,3 };) or tables of data, or databases: these are all well-defined data structures.
Data Structures and organizing data will require students to become more algorithmic in coding.

Data Structure Algorithms

There are many algorithms for different purposes and they interact with different data structures.
Think of algorithms as dynamic underlying pieces that interact with data structures.

EX:

public void swapToLowHighOrder(IntByReference i) {
      if (this.value > i.value) {
          int temp = this.value;
          this.value = i.value;
          i.value = temp;
      }
  }

Together, data structures and algorithms combine and allow programmers to build whatever computer programs they’d like.
Good managed data structures and algorithms ensures well-optimized and efficient code.
Paradigms

Imperative Paradigms
An imperative program consists of commands for the computer to perform to achieve a result. Imperative programming focuses on describing “how” a program code works.
OO Paradigm
OOP models complex things as reproducible, simple structures.
Reusable, OOP classes can be used across programs by simply making an object.
We have learned about many key aspects of OOP.

OO based matrix alteration

public String reverse() {
      // outer loop starting at end row
      StringBuilder output = new StringBuilder();
      for (int i = matrix.length;  0 < i; i--) {
          // inner loop for column
          for (int j =  matrix[i-1].length; 0 < j; j--) {
              output.append((matrix[i-1][j-1]==-1) ? " " : String.format("%x",matrix[i-1][j-1])).append(" ");
          }
          output.append("\n"); // new line
      }
      return output.toString();
  }

Tech Talk Notes

Tech Talk 3

Bubble Sort

Implementation

Selection Sort

Implementation

Merge Sort

Implementation

Insertion Sort

Implementation

(TPT) Study Group Challenge 2

Tri 3: Tech Talk 2: Calculator

Tech Talk 1

Linked Lists

Tech Talk 0

Data Structures

Data Structure Algorithms

Paradigms

Imperative Paradigms

OO Paradigm